[BOJ/백준] 2293. 동전 1 (Python)

🔎 문제

🔗 백준 2293번 동전 1

💡 풀이

DP문제이다. N원의 경우의 수를 구하기 위해 N-1원의 경우의 수를 이용해 풀기 때문이다. 차근차근 따져보자.

과정

먼저 1원, 2원 3원 .. N원 모두 1원짜리 동전으로만 만들수 있는 경우의 수는 1가지(1, 1+1, 1+1+1 …) 이다. 이를 표로 나타내면 이렇게 된다.

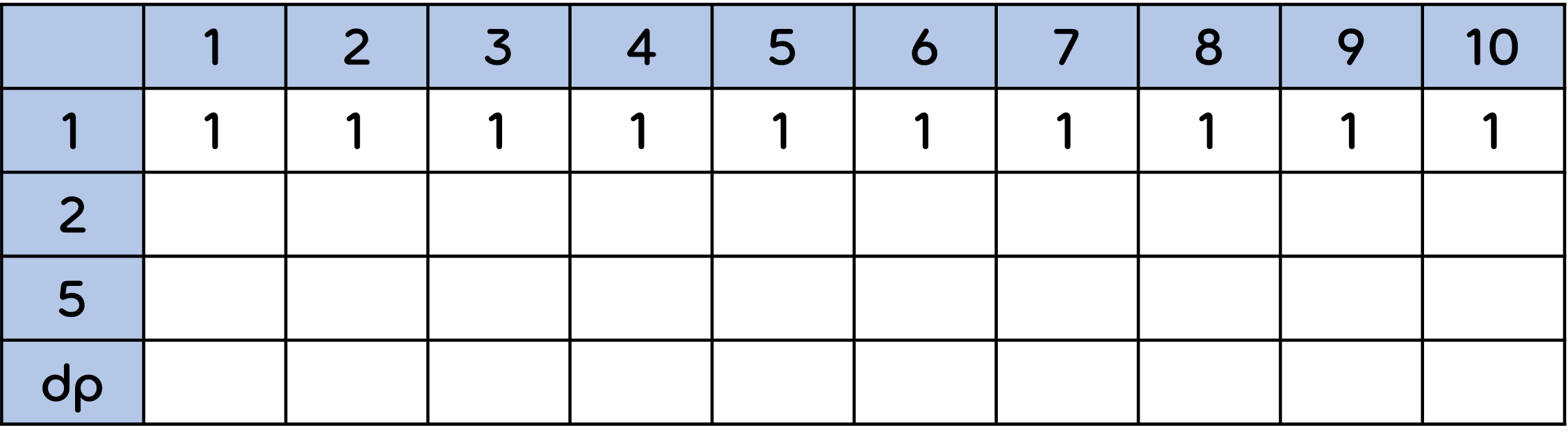
그 다음, 2원에 대해서도 생각해보자.

일단 2원으로 1원을 나타낼 수 있는 경우의 수는 0이다.
그리고 2원으로 2원을 나타낼 수 있는 경우의 수는 1이다.
또, 5원은 4원짜리 동전까진 경우의 수가 0이다.

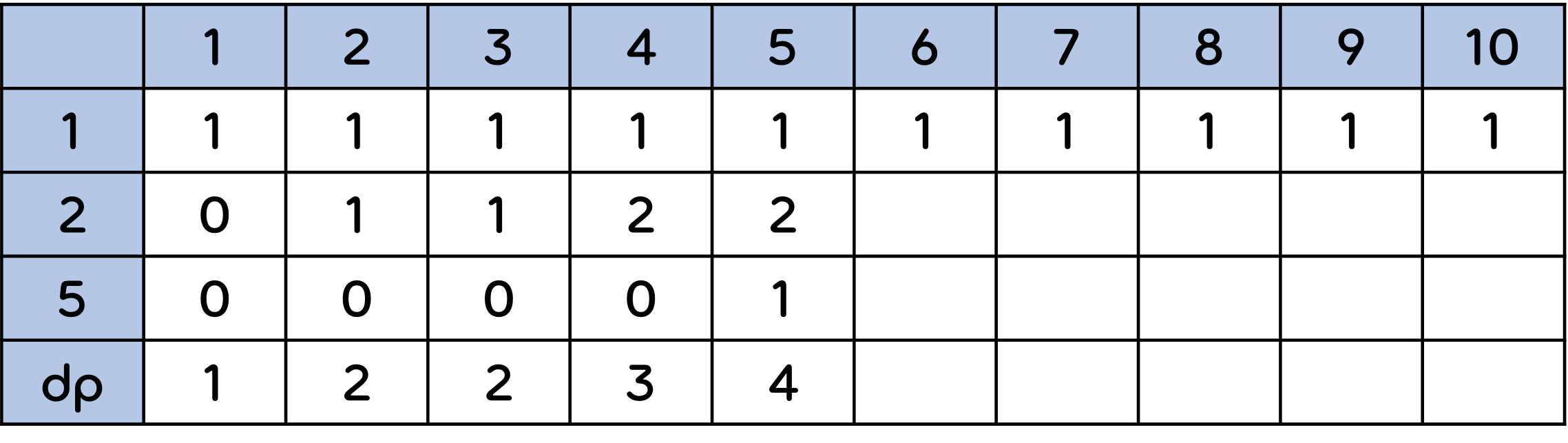
이를 표로 나타내면 아래와 같으며, dp는 해당 열의 합산 값 즉 N원을 구하기 위한 경우의 수가 된다.

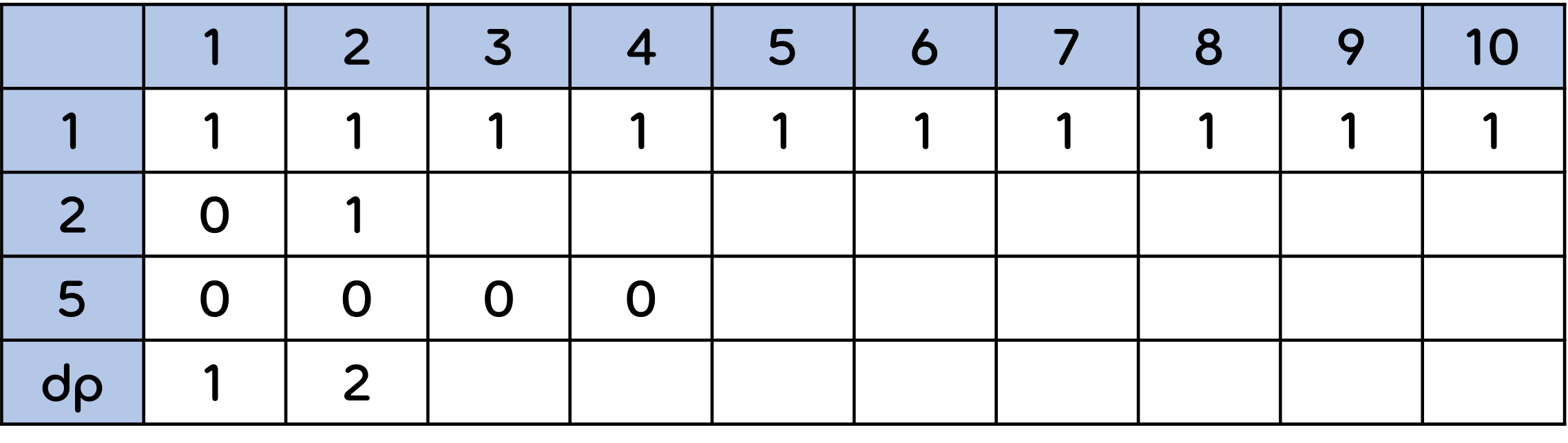
자 그럼 3원을 2원으로 만들 수 있는 경우의 수를 생각해보자. 이때 앞에서 구한 결과들을 최대한 활용한다.

[3 - 2]원 = [구하고자 하는 돈 - 동전의 가치] = 1원을 만드는 경우의 수는 1이다. 1원을 만드는 경우의 수에서 2원 하나만 더 보태면 그것은 3원을 만드는 경우의 수가 된다.

1원을 1원, 2원으로 만드는 경우의 수는 1 + 0 = 1 이므로 3원을 2원으로 만드는 경우의 수는 1이된다. 따라서 dp값은 1 + 1 + 0 = 2 가 된다.

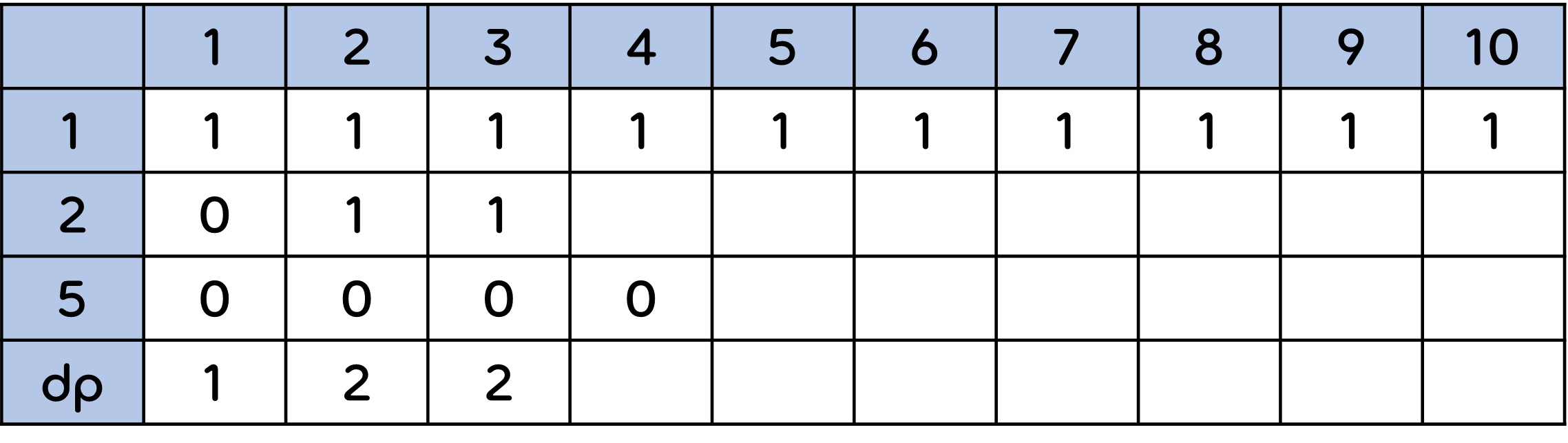
4원을 2원으로 만드는 경우의 수도 [4 - 2]원 = [구하고자 하는 돈 - 동전의 가치] = 2원 의 경우의 수를 이용한다. 2원을 만드는 경우의 수에서 2원 하나만 더 보태면 그것은 4원을 만드는 경우의 수가 된다.

2원을 1원, 2원으로 만드는 경우의 수는 1 + 1 = 2 이므로 4원을 2원으로 만드는 경우의 수는 2가 된다. 따라서 dp값은 1 + 2 + 0 = 3이 된다.

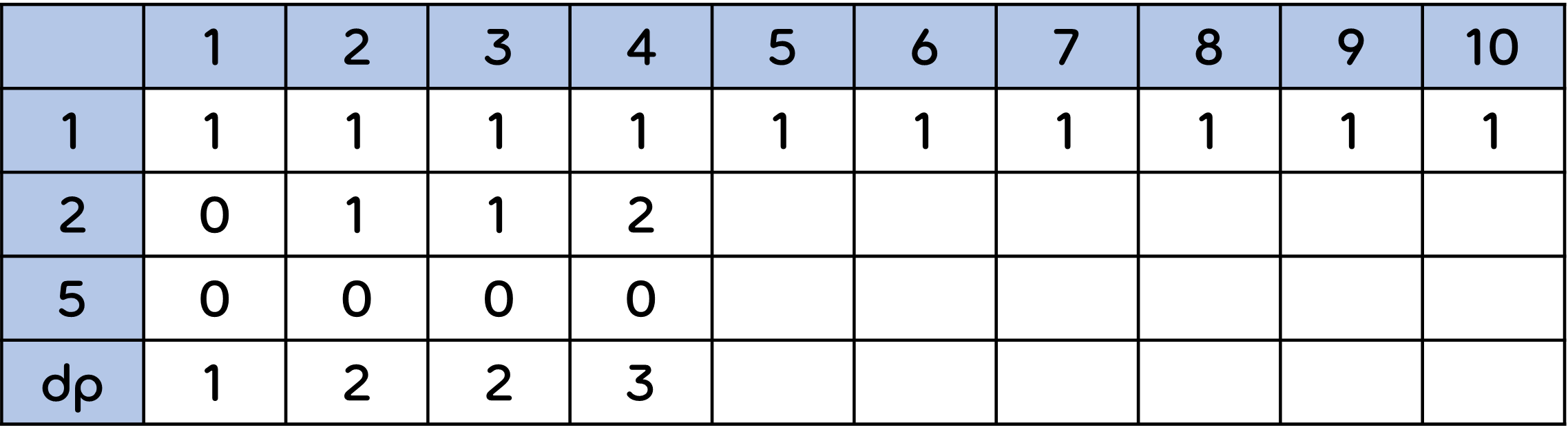
5원을 2원으로 만드는 경우의 수는 똑같이 [5 - 2]원 = [구하고자 하는 돈 - 동전의 가치] = 3원 의 경우의 수를 이용한다. 3원을 만드는 경우의 수에서 2원 하나만 더 보태면 그것은 5원을 만드는 경우의 수가 된다.

3원을 1원, 2원으로 만드는 경우의 수는 1 + 1 = 2 이므로 5원을 2원으로 만드는 경우의 수는 2가 된다. 또, 5원을 5원으로 만드는 경우의 수는 1이므로 최종 dp값은 4가 된다.

이쯤되면 점화식을 세울 수 있게 된다.

점화식

dp[index] = dp[index] + dp[index - values[index]]
     1          2                 3
# 설명
1 : 구하고자 하는 dp[index]값.
2 : 해당 동전의 가치에 대한 경우의 수를 구하기 전 dp[index] 합산 값.
    예를들어 3원을 2원으로 만드는 경우의 수를 구하기 전 3원을 1원으로 만드는 경우의 수는 1이므로
    2원으로 만드는 경우의 수를 구하기 전 dp값은 1이다.
3 : 구하고자 하는 돈에서 동전의 가치를 뺀 값의 dp값.

⬇️ 완성된 dp 테이블

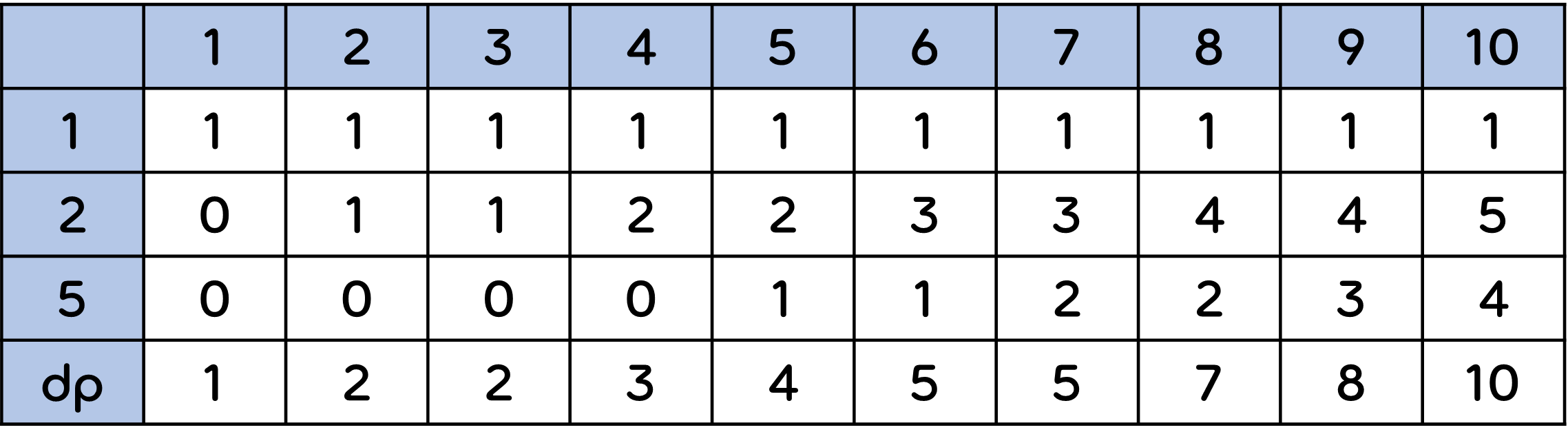
📃 소스코드

구현에 대한 설명은 주석으로 달아 놓았다.

import sys
input = sys.stdin.readline
           
n, k = map(int, input().split())
values = [int(input().strip()) for _ in range(n)]

dp = [0] * (k + 1) # 0 ~ K 원까지 구하기 때문에
                   # 길이가 K + 1인 리스트 만듦
dp[0] = 1          # 1-1원, 2-2원, 5-5원 처럼
                   # 나 자신에 대한 dp값 구하기 위함

for i in range(n): # 동전의 가치 for문
    # 5원을 만드는 경우의 수라 하면,
    # 4원까지는 0이기 때문에 values[i] 부터
    for j in range(values[i], k + 1):
        dp[j] += dp[j - values[i]]

print(dp[k])

카카오페이로 커피사기 ❤️ 토스,계좌로 커피사기 ❤️